Calcul théorique de la turbine


La figure ci-dessous représente les triangles des vitesses à l'entrée (1) et à la sortie (2) d'un auget.
triangles des vitesses

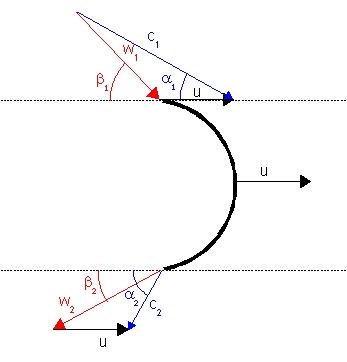
u désigne la vitesse périphérique (ou tangentielle) de l'auget,
c1 et c2 désignent les vitesses absolues de l'eau à l'entrée et à la sortie de la roue,
w1 et w2 désignent les vitesses relatives de l'eau par rapport à l'auget, en entrée et sortie de celui-ci.

Le théorème d'Euler permet de calculer la force F qu'exerce l'eau sur l'auget : \rho \cdot Q \cdot \left(\vec{w}_2-\vec{w}_1 \right)=-\vec{F}

Mais d'après la loi de composition des vitesses on a : \vec w_1=\vec c_1-\vec u. D'où \vec F=\rho\cdot Q\cdot (\vec c_1-\vec u -\vec w_2)

En projetant sur la tangente à la roue (direction de u), on obtient : F=\rho\cdot Q\cdot (c_1\cos\alpha_1-u+w_2\cos\beta_2)

De plus, les chocs et les frottements freinant l'écoulement entre l'entrée et la sortie de l'auget, on peut écrire : w_2=k \cdot w_1
alors : \bg_white F=\rho\cdot Q\cdot (c_1 \cos \alpha_1-u +k\cdot w_1\cos\beta_2)

Si D est le diamètre de la roue, mesuré au centre des augets, le couple T exercé sur la roue a pour expression :

\bg_white T=F\cdot {D\over 2}=\rho\cdot Q\cdot{D\over 2}\cdot (c_1\cos \alpha_1-u+k\cdot w_1\cos\beta_2)
D'où la puissance fournie :
\bg_white P= T\cdot \omega =\rho\cdot Q\cdot{D\over 2}\cdot \omega \cdot(c_1\cos \alpha_1-u+k\cdot w_1\cos\beta_2) où \bg_white \omega est la vitesse angulaire de la roue (rad/s).
Mais \bg_white {D\over 2}\cdot \omega=u donc finalement :

\bg_green P=\rho\cdot Q\cdot u\cdot (c_1\cos\alpha_1-u+k\cdot w_1\cos\beta_2) avec \bg_green w_1=\sqrt{c_1^2+u^2-2u\cdot c_1\cos\alpha_1} d'après le triangle des vitesses à l'entrée (1) de l'auget.
Telliez | le 30/11/2008 à 11:52 |
<   November 2008   >
LunMarMerJeuVenSamDim
     12
3456789
10111213141516
17181920212223
24252627282930